Answer:
C = 14
Explanation:
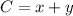
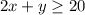
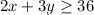
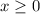

If we graph the inequalities, the solution set of the constraints is the shaded area (see attached diagram).
The vertices of the shaded area are (0, 20), (6, 8) and (18, 0)
To determine the minimum value of C, substitute the values of x and y of each vertex into C = x + y:
at (0, 20): C = 0 + 20 = 20
at (6, 8): C = 6 + 8 = 14
at (18, 0): C = 18 + 0 = 18
Therefore, the minimum value is at (6, 8) ⇒ C = 14