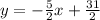Solution
Given triangle ABC with A(3,8), B(7,5), and C(2,3).
Draw the triangle
Calculate the slope of BC
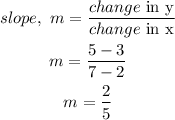
Since the line is perpendicular to BC, then the product of the line and line BC = -1

The line passes through point A(3,8)

Therefore the required equation is: