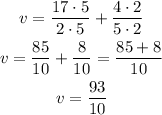The expression is

To solve for v, you have to isolate the variable in one side of the equal sign. To pass "-4/5" to the right side you have to perform the inverse operation to both sides of the expression:
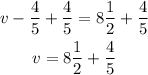
Next is to add both fractions.
First write the mixed fraction as an improper fraction
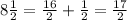
Next find the common denominator between both fractions. For 2 and 5, the common denominator is 10.
So multiply the first fraction by 5 (both numerator and denominator) and the second fraction by 2, this way both will be expressed with the same denominator.