Question

shipAcellusFind the area of the yellow region.Round to the nearest tenth.Help Resources.6 in-6 inArea = [ ? ] in?

Answer 1

To find this area, we need to calculate the area of the square first. Then, we need to calculate the area of the two semicircles. The final value is the area of the square minus the area of the circles. The result must be divided by 2 (since we have a half to find). Then, we can proceed as follows:

Area of the square

`A_{\text{square}}=6in\cdot6in\Rightarrow A_s=36in^2`

Area of the circle

Since we have two semicircles, they form a complete circle. Therefore, the area of the circle is given by:

`A_{\text{circle}}=\pi\cdot r^2\Rightarrow r=(6in)/(2)\Rightarrow r=3in`

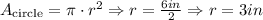
Then, we have:

`A_{\text{circle}}=\pi\cdot(3in)^2\Rightarrow A_(circle)=28.2743338823in^2`

Thus, the resulting area will be:

`A_{\text{yellow}}=(1)/(2)(A_s-A_c)\Rightarrow A_(yellow)=(1)/(2)(36in^2-28.2743338823in^2)=3.86283305885in^2`

Rounding this area to the nearest tenth, we have that the yellow area is equal to 3.9 square inches.