Question

A social media website had 500,000 followers in 2012. The number of followers increases by 19% each year,a. Write an exponential growth function that represents the number of followers I years after 2012b. How many people will be following the website in 2019? Round your answer to the nearest thousand.

Answer 1

Given data:

The initial numbers of follower areA=500,000.

The rate at which followers increases is r=19% =0.19.

(a)

The expression for the exponential growth model is,

`F=A(1+r)^t`

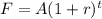
Substitute the given values in the above expression.

`\begin{gathered} F=(500,000)(1+0.19)^t \\ =500,000(1.19)^t \end{gathered}`

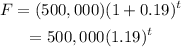
(b)

The value of time is 7 in the year 2019, substitute 7 for t in the above expression.

`\begin{gathered} F=500,000(1.19)^7 \\ =1689,657.7 \\ \approx1690,000 \\ \end{gathered}`

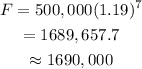
Thus, the expression for the exponential model is f=500,000(1.19)^t, and the followers in the year 2019 is 1690,000.