Given: The data below
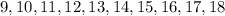
To Determine: The range, population variance and population standard deviation
Solution
The range of a data set is the difference between the largest number and the smallest number in the data set. Therefore
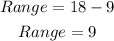
The population variance of a data set can be calculated using the formula below
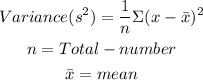
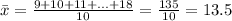
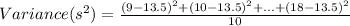
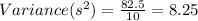
The population standard deviation is
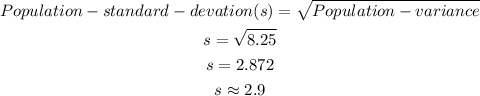
Hence:
Range = 9
Population variance = 8.25
Population standard deviation = 2.9