Let the number of orders served by Mai, Abdul, and Chris be represented by M, A, and C respectively.
A total of 111 orders were served. Thus,
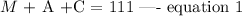
Abdul served 3 times as many orders as Chris. Thus,
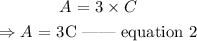
Mai served 6 more orders than Chris. Thus,
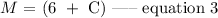
Substitute equations 2 and 3 into equation 1. Thus, we have
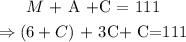
Simplify by opening the brackets
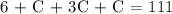
Collect like terms, we have
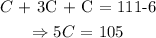
Solve for C dividing both sides of the equation by the coefficient of C.
The coefficient of C is 5. Thus,
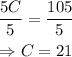
Solve for A by substituting the value of 21 for C in equation 2.
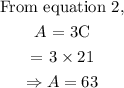
Solve for M by substituting the value of 21 for C in equation 3.
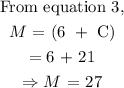
Hence,
number of orders served by Mai = 27
number of orders served by Abdul = 63
number of orders served by Chris = 21