Question

Help me finish this pythagorean theorem model problem I can't understand it

Answer 1

Let's rotate and redraw the figure to make it easier to understand:

The figure appears to be a right triangle with its hypotenuse and opposite side given.

Since this is a right triangle, to be able to get the measurement of the adjacent side, we will be using the Pythagorean Theorem:

`a^2+b^2=c^2`

The formula for the adjacent side or c is:

`a^2+b^2=c^2`
`b^2=c^2-a^2`

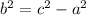
Let's now plug in the given values to get b.

`b^2=c^2-a^2`

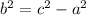
Given: c² = 225 and a² = 145

`b^2=225\text{ - 145}`
`b^2=80`
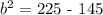
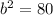
`b\text{ = }\sqrt[]{80}\text{ = }\sqrt[]{16\text{ x 5}}\text{ = 4}\sqrt[]{5}`