Question

At the surface of the ocean, the water pressure is the same as the air pressure above the water, about 15 lblin^2, below the surface the water pressure increases by about 4.54 lblin^2 for every 10ft of descent. F(x) which expresses the water pressure in pounds per square inch as a function of the depth in inches below the ocean surfaces. F(x) = _________ At what depth is the pressure 80 lblin^2? Include the units in the answer: __________

Answer 1

The pressure above the water is 15 lb/in^2 and for every 10 ft, the pressure rises 4.54 lb/in^2

The equation would be:

`f(x)=4.54(lb)/(IN^2)\cdot10ft\cdot x+15(lb)/(IN^2)`

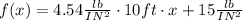
If x = 0, the pressure in the surface is 15 lb/in^2, for each 10 ft of x, the pressure rises 4.54 lb/in^2

Now to solve when the pressure is 80 lb/in^2, we subtitute in the equation:

`80(lb)/(IN^2)=4.54(lb)/(IN^2)\cdot10ft\cdot x+15(lb)/(IN^2)`

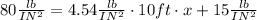
And solve for x:

`\begin{gathered} (80-15)(lb)/(IN^2)=4.54\frac{lb}{\text{IN}^2}\cdot10ft\cdot x \\ (65(lb)/(IN^2))/(45(lb)/(IN^2)\cdot10ft)=x \\ (1.4317)/(ft)=x \\ \end{gathered}`

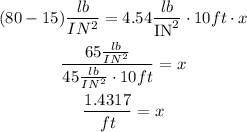
Then the answer to question 2 is 1.43ft

This is basically a linear equation. The slope is the 4.54lb/in^2 for each 10ft. Then we need to adjust the 10ft of x, to reprensents each step of 10 ft for x. And we need to add the 15lb/in^2 for the surface pressure. With all this, we can construct the function of the pressure dependant of the deepness x.