Question

if a savings account starts with $5,000 and Grows by 5% each year how much will be in the account after 12 years

Answer 1

In this case, we can apply the formula for the future value of an investment, which is:

`FV=PV(1+I)^n`

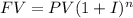
Where FV is the future value, PV is the principal value = $5,000, I is the interest rate in decimal form I=5%/100%=0.05 and n is the number of compounding periods, n=12.

By replacing these values in the formula we obtain:

`\begin{gathered} FV=5000(1+0.05)^(12) \\ FV=5000(1.05)^(12) \\ FV=5000\cdot1.796 \\ FV=8979.28 \end{gathered}`

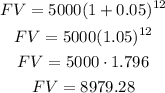
So, after 12 years there will be $8979.28 in the savings account.