Question

PLZ HELP ME OUTTTTTTTTT
66 points

Answer 1

The vertex is at
`(0, -9)`

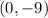
The axis of symmetry
`x = 0`

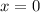
Explanation:

Note: You can answer all the questions looking at the graph

We have the function
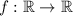`f: \mathbb{R} \rightarrow\mathbb{R}`(I am assuming this) such that
`f(x) = y = (x-3)(x+3)`

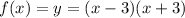
We note that

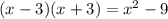`(x-3)(x+3) = x^2-9` once we have a difference of squares

Therefore, we have a quadratic function.

So

`y = x^2-9`

The vertex
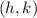`(h, k)` is

`h = (-b)/(2a) = (-0)/(2 \cdot 1) = 0`

`k= h^2 - 9 = 0^2 - 9 =-9`

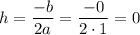
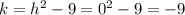
Therefore, the vertex is at
`(0, -9)`

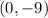
As we know the vertex, we conclude that the axis of symmetry
`x = 0`

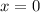
The x-intercepts occur at
`y = 0`

`y = (x-3)(x+3) \implies x = -3, x=3`

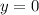
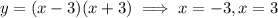
So, the left x-intercept is
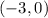`(-3, 0)` and the right x-intercept is
`(3, 0)`

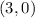
As I stated in the beginning, the domain is the set of all real numbers. Precisely,

`Dom(f) = \mathbb{R} = (-\infty, \infty)`

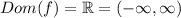
Once, we know the vertex, we also conclude that the Range is

`Ran(f)= [-9,\infty)`

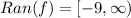
Greater than or equal to -9