Question

Select the correct answer1 - quadratic, linear, exponential2 - 1.5, 18, 16, 123 - 16, 12, 20, 184 - 18, 6, 20, 12

Answer 1

1 - The equation is:

`p(x)=-0.5x^2+6x`

Since it has no variable on exponents and it has a term with x to the second power, this is a quadratic function.

2 - x represents the length of the tomato patch, so if we want the area of the bell pepper patch, we can input x = 8 into the function:

`\begin{gathered} p(8)=-0.5\cdot8^2+6\cdot8 \\ p(8)=-0.5\cdot64+48 \\ p(8)=-32+48 \\ p(8)=16 \end{gathered}`

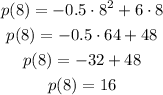
Thus, the area is 16 square feet.

3 - Since the leading coefficient is negative, the vertex of the parabola gives the maximum value for the function.

The x value of the vertex is:

`\begin{gathered} ax^2+bx+c \\ x_v=-(b)/(2a) \end{gathered}`

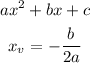
So, in this case:

`x_v=-(6)/(2\cdot(-0.5))=-(6)/(-1)=6`

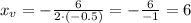
And to find the value for the area, we need to input that into the function:

`\begin{gathered} p(6)=-0.5\cdot6^2+6\cdot6 \\ p(6)=-0.5\cdot36+36 \\ p(6)=-18+36 \\ p(6)=18 \end{gathered}`

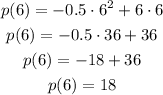
Thus, the maximum area is 18 square feet.

4 - The value for the length of the tomato patch is just the corresponding x for this maximum, which we calculated as the vertex x:

`x_v=6`

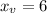
Thus, the length of the tomato patch for this maximum value is 6 feet.