Given:
The given function f(x) approaches 0.5 when x approaches 1 from the left.
The given function f(x) approaches 1.5 when x approaches 1 from the right.
Required:
We need to find the limit of f(x).
Step-by-step explanation:
There is a jump discontinuity.
The given function f(x) approaches 0.5 when x approaches 1 from the left.
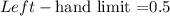
The given function f(x) approaches 1.5 when x approaches 1 from the right.
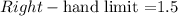
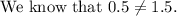
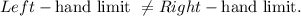
The limit does not exist at x =1 in the given graph.
Final answer:
The limit does not exist at x =1 in the given graph because the left hand-limit is not equal to the right-hand limit.