Question

A pedestrian walked one third of the total distance at speed 2 mph, the secondthird at speed 3 mph, and the remainder of the distance at the speed that is equal to the average speed overthe entire trip. Find that average speed.

Answer 1

Let's use the variable x to represent the average speed and d to represent the total distance.

Then, let's calculate the time needed for each part:

The first third has a speed of 2 mph, so the time is:

`\begin{gathered} \text{distance}=\text{speed}\cdot\text{time} \\ (d)/(3)=2\cdot t \\ t=(d)/(6) \end{gathered}`

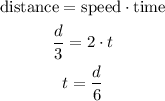
For the second third, we have a speed of 3 mph, so:

`\begin{gathered} (d)/(3)=3\cdot t \\ t=(d)/(9) \end{gathered}`

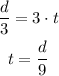
The last third has a speed of x, so:

`\begin{gathered} (d)/(3)=x\cdot t \\ t=(d)/(3x) \end{gathered}`

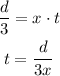
Then, the average speed is the total distance over the total time, so:

`\begin{gathered} x=\frac{d}{t_{\text{total}}} \\ x=(d)/((d)/(6)+(d)/(9)+(d)/(3x)) \\ x=(1)/((1)/(6)+(1)/(9)+(1)/(3x)) \\ x=(1)/((3x+2x+6)/(18x)) \\ x=(18x)/(5x+6) \\ 1=(18)/(5x+6) \\ 5x+6=18 \\ 5x=12 \\ x=2.4 \end{gathered}`

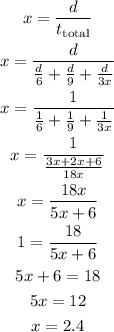
The average speed of the trip is 2.4 m/s.