In order to find by how much is the car magnified, first let's find the position of the image using the formula below:
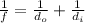
Where f is the focal length, do is the object position and di is the image position.
After converting all measures to meters, we have:
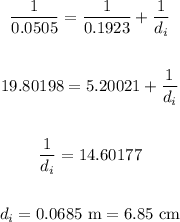
Now, to find the magnification factor, we use the formula below:

The car is magnified by a factor of 0.356 (that is, the image is smaller than the object)
Now, for the second part of the question, let's use the first formula again, with f = 0.0316 m and di = 0.1534 m:
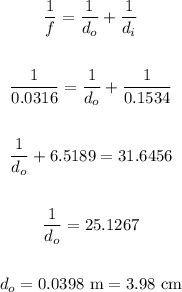
Therefore the object should be put at 3.98 cm.