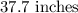Question

A small car has a tire with a 15-inch diameter. A mountain bike has a tire with a 27-inch diameter. How much father than the small car does the mountain bike have to drive for its tire to complete one revolution?

Answer 1

The mountain bike will travel 37.7 inches farther than the small car in one complete revolution.

`37.7\text{ inches}`

Step-by-step explanation:

The distance a tire travel in one complete revolution is equal to the circumference of the tire.

The circumference can be calculated using the formula;

`C=2\pi r=\pi d`

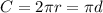
Where;

C = Circumference

r = radius of tire

d = diameter of the tire

For the small car with tire of diameter 15 inches, the distance travelled in one revolution is;

`\begin{gathered} C_1=\pi d_1=\pi(15)=15\pi \\ C_1=47.12\text{ inches} \end{gathered}`

For the mountain bike with tire of diameter 27 inches, the distance travelled in one revolution is;

`\begin{gathered} C_2=\pi d_2=\pi(27)=27\pi_{} \\ C_2=84.82\text{ inches} \end{gathered}`

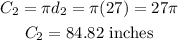
The difference between the distance travelled in one complete revolution is;

`\begin{gathered} \Delta C=C_2-C_1=84.82-47.12 \\ \Delta C=37.70\text{ inches} \end{gathered}`

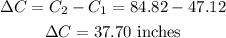
Therefore, the mountain bike will travel 37.7 inches farther than the small car in one complete revolution.

`37.7\text{ inches}`