Question

The System of PolynomialsYou are aware of the different types of numbers: natural numbers, integers, rational numbers, and real numbers. Now you will work with a property of the number system called the closure property. A set of numbers is closed for a specific mathematical operation if you can perform the operation on any two elements in the set and always get a result that is an element of the set.Consider the set of natural numbers. When you add two natural numbers, you will always get a natural number. For example, 3 + 4 = 7. So, the set of natural numbers is said to be closed under the operation of addition.Similarly, adding two integers or two rational numbers or two real numbers always produces an integer, or rational number, or a real number, respectively. So, all the systems of numbers are closed under the operation of addition.Think of polynomials as a system. For each of the following operations, determine whether the system is closed under the operation. In each case, explain why it is closed or provide an example showing that it isn’t.1. AdditionType your response here:2. SubtractionType your response here:3. MultiplicationType your response here:4. DivisionType your response here:

Answer 1

Polynomials are closed under the operation of addition, subtraction, and multiplication only. Here's why:

1. Addition: (Closed)

Reason: Say we have two polynomials: (x⁴ + 2x³ - 4) and (3x³ - 2x² + 6x). If we add these two polynomials, (x⁴ + 2x³ - 4) + (3x³ - 2x² + 6x), it will result to x⁴ + 5x³ - 2x² + 6x - 4 which is also a polynomial.

When adding polynomials, the variables and the exponents don't change. This guarantees that the sum of these variables with exponents will always be a polynomial.

2. Subtraction: (Closed)

Reason: Say we have two polynomials: (x⁴ + 2x³ - 4) and (3x³ - 2x² + 6x). If we subtract these two polynomials, (x⁴ + 2x³ - 4) - (3x³ - 2x² + 6x), it will result to x⁴ - x³ + 2x² - 6x - 4 which is also a polynomial.

When subtracting polynomials, the variables, and the exponents don't change. This guarantees that the difference of these variables with exponents will always be a polynomial.

3. Multiplication: (Closed)

Reason: Say we have two polynomials (x + 2) and (x - 4). If we multiply these two polynomials, (x + 2)(x - 4), it will result in x² - 2x - 8, which is also a polynomial.

When multiplying polynomials, the variables do not change but the exponents will be added to each other. In this case, we can guarantee that the new exponents will be positive whole numbers still and this guarantees that the answer will be a polynomial.

4. Division: (Not closed)

Reason: When dividing polynomials, exponents are being subtracted from each other, therefore, we might have a result of a negative exponent. Negative exponents are not allowed in a polynomial. Example, say we have two polynomials (x²) and (x⁴), if we divide (x²) by (x⁴), the resulting value would be:

`(x^2)/(x^4)=x^(-2)`

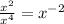
The resulting value is x to the power of negative 2, and is not a polynomial.