Question

Need help finding how the graph would look like please! Thankyou!

Answer 1

- We are asked to plot the function below:

`y=\cos((1)/(4)x)`

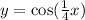
- The general formula for the cosine function is:

`\begin{gathered} y=A\cos(Bx+C)+D \\ where, \\ (2\pi)/(T)=B \\ \\ T=\text{ Period} \end{gathered}`

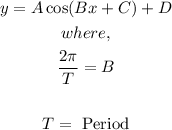
- Comparing this general formula to the question, we have;

`\begin{gathered} (2\pi)/(T)=(1)/(4) \\ \\ \therefore T=2\pi*4 \\ T=8\pi \end{gathered}`

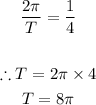
- This implies that the period is 8π. Thus, our graph should stop at 8π.

- We have 4 divisions along the x-axis, thus, each division must be

`(8\pi)/(4)=2\pi`

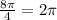
- Plotting the graph, we have: