Question

Logarithmsin a research laboratory, biologist studied the growth of a culture of bacteria. From the data collected hourly, they concluded that the culture increases in number according to the formula N(t)=45(1.85)t where N is the number of bacteria present and t is the number of hours since the experiment beganUse the model to calculatea) the number of bacteria at the start of the experiment.b) number of bacteria present after 4 hours, giving your answer to the nearest whole number of bacteria.c) the time it would take for the number of bacteria to reach 1000.

Answer 1

Growth of Culture of bacteria increases in number according to the formula :

`N(t)=45(1.85)^t`

N = Number of bacteria present

t = number of hours from the initial state.

a) number of bacteria at the start of the experiment.

In the begining when the expreiment start, the time is zero

t = 0

Substitute t = 0 in the growth expression of bacteria

`\begin{gathered} N(t)=45(1.85)^t \\ N(0)=45(1.85)^0 \\ as\colon a^0=1 \\ N(0)=45(1) \\ N(0)=45 \end{gathered}`

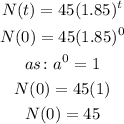
When the experiment start, number of bacteria is 45

b) number of bacteria present after 4 hours, giving your answer to the nearest whole number of bacteria.

After fours hours, i.e. t = 4

Substitute t = 4 in the growth expression of bacteria

`\begin{gathered} N(t)=45(1.85)^t \\ N(4)=45(1.85)^4 \\ N(4)=45*11.7135 \\ N(4)=527.1077 \\ N(4)=527 \end{gathered}`

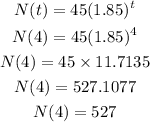
Number of bacteria after 4 hours are 527

c) the time it would take for the number of bacteria to reach 1000.​

Here, we have number of bacteria 1000 i.e. N = 1000

Substitute the value and solve for t:

`\begin{gathered} N(t)=45(1.85)^t \\ 1000=45(1.85)^t \\ (1000)/(45)=1.85^t \\ 1.85^t=(200)/(9) \\ 1.85^t=22.22 \\ \text{Taking log on both side: } \\ t\ln (1.85)=\ln (22.22) \\ t=(\ln (22.22))/(\ln (1.85)) \\ t=5.0409 \\ t=5 \end{gathered}`

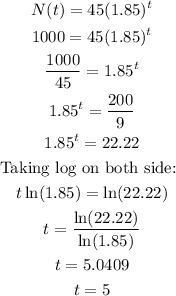
It will take 5 years to reach upto 1000 bacteria

Answer:

a) Number of bacteria at the start of experiment 45

b) Number of bacteria after 4 hours 527

c) It would take 5 years to reach upto 1000 bacteria