Answer:
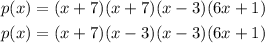
Explanation:
If a 4th degree has only the following roots: x=−7,x=3,x=−1/6.
A 4th-degree polynomial must have 4 roots. What this means is that one of the roots is a repeated root.
If -7 is the repeated root, an example of such polynomial is:

The given polynomial is not the only 4th-degree polynomial that has only these roots. Any of the given roots can be the repeated root.
If on the other hand, 3 is the repeated root, then p(x) will be:
