Question

A recent math test had an average score of 75, with a standard deviation of 10. What percentage of people passed the test (i.e. scored a 70 or higher)?

Answer 1

We have to find the z-score at first, then use it to find the percentage of 70 or higher

The rule of the z-score is

`z=(x-\mu)/(\sigma)`

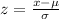
μ is the mean

σ is the standard deviation

Since the average score is 75, then

`\mu=75`

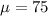
Since the standard deviation is 10, then

`\sigma=10`

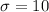
Since we need the percentage of 70, then

`x=70`

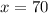
Substitute them in the rule above to find z

`\begin{gathered} z=(70-75)/(10) \\ z=-(5)/(10) \\ z=-0.5 \end{gathered}`

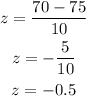
Now, we will search in the table for the value of -0.5

The value of -0.5 is 0.30854

Since we need the percentage of 70 or higher, then

`\begin{gathered} P(x\ge70)=1-P(x) \\ P(x\ge70)=1-0.30854 \\ P(x\ge70)=0.69146 \end{gathered}`

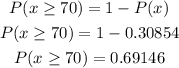
Change it to percent

`\begin{gathered} P(x\ge70)=0.69146*100\text{ \%} \\ P(x\ge70)=69.146\text{ \%} \end{gathered}`

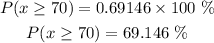
The percentage of 70 or higher is about 69.15%