Part 1
Simple interest
we know that
The simple interest formula is equal to
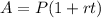
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest
t is Number of Time Periods
in this problem we have
P=$1,500
r=7.5%=0.075
t=4 years
substitute in the formula
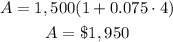
Part 2
The compound interest formula is equal to

where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
P=$1,500
r=7.5%=0.075
t=4 years
n=1
substitute
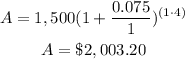
therefore
A better investment is a compound interest
Find out the difference
2,003.20-1,950=$53,20
so
Is earned $53,20 more