Question

the measurements are listed 6,9,2,5,4,10,3,12,2,7,7,8 find the mean median mode range variance and standard deviation

Answer 1

Given:

The measurements are listed 6,9,2,5,4,10,3,12,2,7,7,8 .

Required:

To find mean median mode range variance and standard deviation.

Step-by-step explanation:

(1)

Mean =

`=(6+9+2+5+4+10+3+12+2+7+7+8)/(12)`
`\begin{gathered} =(75)/(12) \\ \\ =6.25 \end{gathered}`

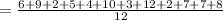
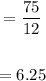
(2)

Median : Is the middle value when the data values have been sorted (or the average of the 2 middle values if there are an even number of data values).

`2,2,3,4,5,6,7,7,8,9,10,12`

Now the middle terms are 6 and 7.

`\begin{gathered} =(6+7)/(2) \\ \\ =6.5 \end{gathered}`

(3)

Mode: Is the data value(s) the occur with the greatest frequency.

Therefore, 2 and 7 are modes.

(4)

Range:

Range shows the mathematical distance between the lowest and highest values in the data set.

Therefore, from the given data 2 is the lowest value and 12 is the highest value,

`\begin{gathered} =12-2 \\ =10 \end{gathered}`

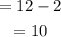
Final Answer:

Mean : 6.25

Median : 6.5

Mode : 2 and 7

Range: 10