Question

Find the volume of this object.Use 3 for a.Volume of a CylinderV=Tr2hVolume of a Sphere3 cmV=Tr34 cm10 cmV~ [?]cm3

Answer 1

Step-by-step explanation

here we have a figure compounded by a sphere and a cylinder, so the total volume of the figure is teh sum of teh Sphere and cylinder areas, so

so

total volume= volume of the cylinder+volume of sphere+

replace

`V_t=(\pi\cdot(r_(cyl))^2\cdot h)+(4)/(3)\pi(r_(sphe)^3)`

so, Let

`\begin{gathered} \text{radius}_(cyl\in der)=(diameter)/(2)=(10)/(2)=5\text{ cm} \\ h=4\text{ cm} \\ \text{and} \\ \text{radius}_{sphere\text{ }}=3\text{ cm} \\ \pi=3 \end{gathered}`

now, replace in the expression

`\begin{gathered} V_t=(3\cdot(5cm)^2\cdot4cm)+(4)/(3)(3)(3^3_{}cm^3) \\ V_t=3\cdot25cm^2\cdot4cm+4(27cm^3) \\ V_t=300cm^(^3)+108cm^3 \\ V_t=408cm^(^3) \end{gathered}`

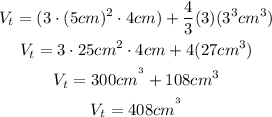
therefore, the answer is

`V_{}\approx408cm^(^3)`

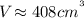
I hope this helps you