Question

The expression defining each function consists of a sum or difference of terms and, as written, the long-term behavior of each function is an indeterminate form (an expression which does not have a defined value without additional information) of the type “∞ - ∞”. Find the long-term behavior of each function by first writing each as a ratio of two polynomials.

Answer 1

Given function is

`y(t)=(t^2+t)/(t+2)-(t^3)/(t+3)`

The lease common multiple of (t+2) and (t+3) is (t+2)(t+3) , making the denominator (t+2)(t+3).

`y(t)=\frac{(t^2+t)(t+3)}{(t+2)(t+3)_{}}-(t^3(t+2))/((t+3)(t+2))`

`y(t)=\frac{t^2(t+3)+t(t+3)}{(t+2)(t+3)_{}}-(t^3(t+2))/((t+3)(t+2))`

`y(t)=\frac{t^3+3t^2+t^2+3t}{(t+2)(t+3)_{}}-(t^4+2t^3)/((t+3)(t+2))`

`y(t)=\frac{t^3+4t^2+3t-t^4-2t^3}{t\mleft(t+3\mright)+2\mleft(t+3\mright)_{}}`

`y(t)=\frac{-t^4-t^3+4t^2+3t}{t^2+3t+2t+6_{}}`

`y(t)=\frac{-t^4-t^3+4t^2+3t}{t^2+5t+6_{}}`

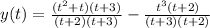
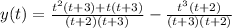
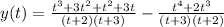
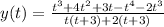
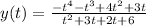
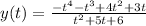
Hence the ratio of two polynomial is

`y(t)=\frac{-t^4-t^3+4t^2+3t}{t^2+5t+6_{}}`

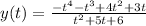
The long term behavior is

`y(t)=\frac{-t^4-t^3+4t^2+3t}{t^2+5t+6_{}}\approx(-t^4)/(t^2)=-t^2`
`\text{ So x }\rightarrow\pm\infty\text{ y likes like y}=-x^2`
`\lim _(n\to\infty)-t^2=-\infty`

`\lim _(n\to-\infty)-t^2=-\infty`

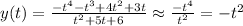
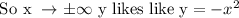
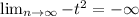
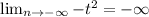
The is not a horizontal line, So this is not horizontal asymptotes.

Hence the asymptotes is oblique.