We have here a multiplication of two complex numbers. However, we can use the following rule to deal with this question:
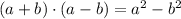
Or equivalently:
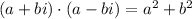
We will do it step by step:
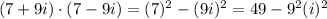
Then, we have that i²=-1.
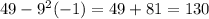
Therefore, we have that:

[Notice that the imaginary part of this complex number is equal to 0i = 0.]