In the present question, there are quadratic expressions presented in two different ways, but equivalent, as the generic one that follows:
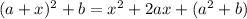
From this, we will try to find the matches for those in the form presented on the left side of the equality by performing the calculation of the square.
The quadratic expression presented in the second rectangle can be written as follows:
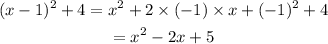
From this, we have the following match!

Now, for the third rectangle, we perform the following calculation using the distributive property:
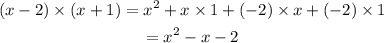
And from this calculation, we found another match, which is the one that follows:
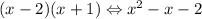
Now, let's move to the second expression among the rectangles in the gray box and perform the proposed calculation using the distributive property again:
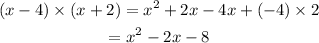
And from this, we can write the following match:
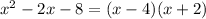
Now, let's develop the last expression in the gray box, which is also the last match:
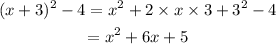
And from this, we conclude the last match, that follows:
