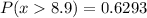Given:
- The Mean:
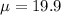
- The Standard Deviation:
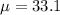
You have to find:
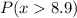
You need to find the z-statistic using this formula:
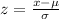
In this case:
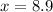
Then:
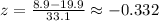
You need to find:
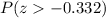
By symmetry, this is equal to:
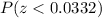
Using the Normal Distribution Table, you get:
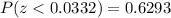
Hence, the answer is: