Question

Blinking is a game in which three dice are rolled. To win the game a player must roll triples that is three of the same number.Jeremy decided to play the game if blink and is determined to play until he wins. Calculate the probability of getting the first win in the third roll. You may either use formula or calculator.How many times can he expect to roll the dice in order to win?

Answer 1

We will have the following:

First, we will have that the total number of outcomes per toss is:

`6\cdot6\cdot6=216`

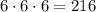
Now, the probability of getting a triple is:

`(6)/(216)=(1)/(36)`

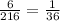
Then, we will have that the probability of not getting a triple is given by:

`(210)/(216)=(35)/(36)`

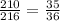
Now, the probability of getting the first win in the third roll is:

`P=(35)/(36)\cdot(35)/(36)\cdot(1)/(36)\Rightarrow P=(1225)/(46656)`
`\Rightarrow P\approx0.026`

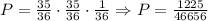
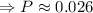
So, the probability is approximately 2.6%.

So, he can expect to roll the dice 35 times before winning.