We have to find the values of x that are solution for the equation
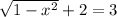
To solve this equation, the first thing we will do is pass, the 2 that is on the left side, to the right side with the opposite sign
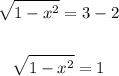
Now we will take power two, on both sides of the equation
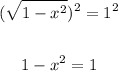
Now we will pass the x square to the rigth with opposite sign, and the 1 on the right to the left with opposite sign

Finally, we take square root on both sides to find
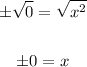
Where we have to include both square roots, the positive and the negative one. In this specific case, both are the same, because the solution is 0. Therefore, we conclude:

We conclude that the provided equation has a unique solution, and that this solution is 0.