Explanation
We are given the following points:
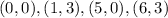
We are required to determine which quadrilateral it is with the given points as vertices.
This is achieved thus:
- The graph of the points is:
- Next, we determine if AB = CD and BC = AD as follows:
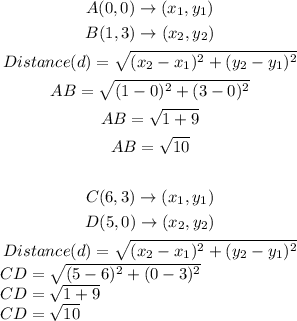
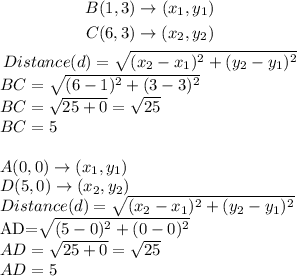
- Using the graph and the distances gotten above, the quadrilateral is a Parallelogram.
Option D is correct.