Question

Hi! I was absent today and did not understand this lesson please I will be really grateful if you help me ! I appreciate it this is classwork assignment does not count as a test, I did the first question and it was right but the second one I do not know how to solve it

Answer 1

sin(α + β) = -84/205

tan(α + β) = 84/187

Step-by-step explanation:

To find sin(α + β), we will use the following identity

`\begin{gathered} \sin ^2\theta+\cos ^2\theta=1 \\ \text{Then} \\ \sin ^2(\alpha+\beta)^{}+\cos ^2(\alpha+\beta)^{}=1 \end{gathered}`

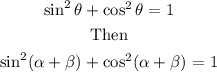
So, solving for sin(α + β), we get:

`\sin (\alpha+\beta)=\pm_{}\sqrt[]{1-\cos^2(\alpha+\beta)}`

Now, we can replace cos(α + β) = -187/205 to get:

`\begin{gathered} \sin (\alpha+\beta)=\pm\sqrt[]{1-((187)/(205))^2} \\ \sin (\alpha+\beta)=\pm(84)/(205) \end{gathered}`

Then, α + β is on quadrant III. It means that the sine of the angle is negative. Therefore

sin(α + β) = -84/205

Finally, to add tan(α + β), we will use the following

`\tan (\alpha+\beta)=(\sin (\alpha+\beta))/(cos(\alpha+\beta))`

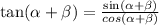
Replacing the values, we get:

`\tan (\alpha+\beta)=(-(84)/(205))/(-(187)/(205))=(-84*205)/(205*(-187))=(84)/(187)`

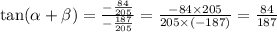
Therefore

tan(α + β) = 84/187