Question

Three masses 2 kg, 3 kg and 1 kg are at (0, 0), (−1, 0) and (1, 1), respectively. Calculatethe center of mass.

Answer 1

Given,

Three masses

m₁=2 kg

m₂=3 kg

m₃=1 kg

The coordinate of mass 1 is (x₁,y₁)=(0,0)

The coordinate of mass 2 is (x₂,y₂)=(-1,0)

The coordinate of mass 3 is (x₃,y₃)=(1,1)

The x-coordinate of the center of mass is given by,

`x=(m_1x_1+m_2x_2+m_3x_3)/(m_1+m_2+m_3)`

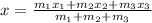
On substituting the known values,

`\begin{gathered} x=(2*0+3*-1+1*1)/(2+3+1) \\ =-(1)/(3) \end{gathered}`

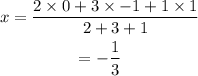
And the y-coordinate of the center of mass is given by,

`y=(m_1y_1+m_2y_2+m_3y_3)/(m_1+m_2+m_3)`

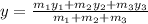
On substituting the known values,

`\begin{gathered} y=(2*0+3*0+1*1)/(2+3+1) \\ =(1)/(6) \end{gathered}`

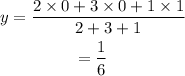
Thus the center of mass is at (-1/3, 1/6)