Question

For each expression below, select the category to which the expression belongs.Select all that apply.1ყ3monomialpolynomialtrinomialnone of thesebinomial3x2 + 5y3trinomialmonomialpolynomialbinomialnone of thesePls see the picture

Answer 1

We are given the following function:

`(1)/(xy^3)`

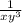
We are asked to determine what type of function is.

An expression of the form:

`ax^my^n\ldots z^l`

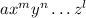
This means a product of constant and variables elevated to different exponents is called a "monomial". If we have the sum of two monomials, like this:

`a_1x^(m1)y^(n1)\ldots z^(l1)+a_2x^(m2)y^(n2)\ldots z^(l2)`

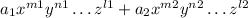
Then, this is called a binomial.

If we have the sum of three monomials, like for example:

`a_1x^(m1)y^(n1)\ldots z^(l1)+a_2x^(m2)y^(n2)\ldots z^(l2)+a_3x^(m3)y^(n3)\ldots z^(l3)`

It is called a trinomial. And if we have more than 3 monomials then it is called a "polynomial".

The given function is the quotient between two functions, therefore, it is not any of the given types of functions.

The given function:

`3x^2+5y^3`

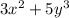
Here, we have two monomials:

`\begin{gathered} 3x^2,\text{ and } \\ 5y^3 \end{gathered}`

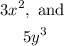
This means that the expression is a binomial.