Question

f(x)= x + 1. Find the domain, range, andintercepts of the function. Then find theminimum and maximum values on the interval[0, 3].

Answer 1

To answer this question, we need to see that this function is a linear function. The domain and range for a linear function, in this case, are:

The Domain and Range of the Function

Domain:

`(-\infty,\infty)`

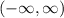
And the Range is also:

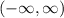
`(-\infty,\infty)`The x- and y-intercepts of the Function

The intercepts of the function are those values for which the function passes through the x- and y-axis. If we need to find the x-intercept, we need to solve the function for y = 0, as follows:

`y=x+1\Rightarrow0=x+1\Rightarrow x=-1`

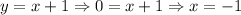
Therefore, the x-intercept is the point (-1, 0).

To find the y-intercept, we need to solve the function when x = 0 as follows:

`y=x+1\Rightarrow y=0+1\Rightarrow y=1`

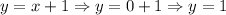
Therefore, the y-intercept is (0, 1).

Finding the minimum and maximum values on the interval [0, 3]

As we can see from the interval notation, we need to find the values of the function at the two extremes of the interval. In this case, we have that we need to find the value of the function when x = 0, and when x = 3.

We have that the function is:

`f(x)=x+1`

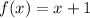
When x = 0, the value of the function is:

`f(0)=0+1\Rightarrow f(0)=1`

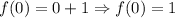
When x = 3, the value of the function is:

`f(3)=3+1\Rightarrow f(3)=4`

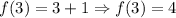
Therefore, on the interval [0, 3] the minimum value of the function is equal to 1 (minimum value = 1). The maximum value of the function is equal to 4 (maximum value = 4).

In summary, we have:

• The domain of the function is (-∞, ∞).

,

• The range of the function is (-∞, ∞).

The intercepts are:

• The x-intercept is the point (-1, 0).

,

• The y-intercept is the point (0, 1).

• The minimum value on the interval [0, 3] is f(0) = 1.

,

• The maximum value on the interval [0, 3] is f(3) = 4.