Question

Vector u has a magnitude of 30 and a direction of 70°. Vector v has a magnitude of 40 and a direction of 220°. What is the direction of u + v? Round to the nearest degree.

Answer 1

Given:

The sketch of the two vectors can be made as shown below;

Resolving the forces into the horizontal and vertical components,

`\begin{gathered} \text{For vector u,} \\ 30\cos 70i+30\sin 70j \\ \\ \text{For vector v,} \\ -40\cos 40i-40\sin 40j \end{gathered}`

Hence, the resultant vector (u + v) is;

`\begin{gathered} u+v=(30\cos 70-40\cos 40)i+(30\sin 70-40\sin 40)j \\ u+v=-20.38i+2.4793j \\ \\ \text{where,} \\ F_x=-20.38 \\ F_y=2.4793 \end{gathered}`

The direction of u + v is given by;

`\begin{gathered} \theta=\tan ^(-1)((F_y)/(F_x))^{}_{} \\ \theta=\tan ^(-1)((2.4793)/(-20.38)) \\ \theta=-6.936 \end{gathered}`

Since the tangent of the angle is negative, then it falls in the second or fourth quadrant.

In the second quadrant,

`\begin{gathered} \theta=-6.936+180 \\ \theta=173.064^0 \\ \\ To\text{ the nearest degre}e,\text{ the direction of u + v is 173 degr}ees \end{gathered}`

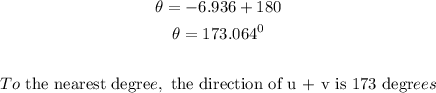
Therefore, the direction of u + v to the nearest degree is 173 degrees.