We are given the following function
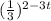
Let us re-write this function in the following form.
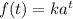
Where k is a constant.
Step 1:
Split the powers using the multiplication rule of exponents.
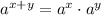
Applying the above rule, the function becomes
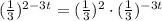
Further simplifying, the function becomes
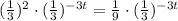
Step 2:
Apply the power rule of exponents
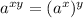
So, the function becomes
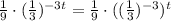
Further simplifying the function becomes

Therefore, the function is
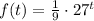
Where k = 1/9 and a = 27