The two diagrams are two graphs with different gradients. The gradient of a graph is a measure of change on the y axis with respect to change on the x-axis.
Typically, a graph that goes upwards from left to right has a positive gradient and that which goes downwards from left to right has a negative gradient (this will be proven).
The steps to finding the gradient of any straight-line graph are to select two points and apply the following operation on their coordinates.
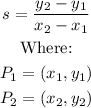
Now, on our graphs, we will perform this operation.
Graph 1:
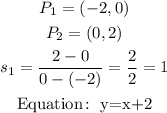
Graph 2:
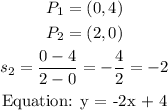
This further buttresses our point about what graph produces a positive gradient.
Graph 1 is such that there is an equal increase on the y-axis with respect to the x-axis
Graph 2 is such that for any increase on one axis, there is a double decrease on the other.