Question

As a tornado moves, its speed increases. The function S(d) = 93logd + 65 relates the speed of the wind, S, in miles per hour, near the centre of a tornado to the distance that the tornado has travelled, d, in miles. Calculate the average rate of change for the speed of the wind at the centre of a tornado from mile 10 to 100

Answer 1

Given that;

As a tornado moves, its speed increases, the function is shown below;

`S(d)=93logd+65`

To calculate the average rate of change for the speed of the wind at the centre of a tornado,

a) For the rate of change for the speed of the wind at the centre of a tornado from mile 10 to 100,

Where, d = 10,

`\begin{gathered} S(10)=93\log_(10)\left(10\right)+65 \\ S(10)=93+65=158\text{ miles/hour} \end{gathered}`

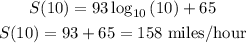
Where, d =100

`S(100)=93\log_(10)\left(100\right)+65=2(93)\log_(10)10+65=186+65=251\text{ miles/hour}`

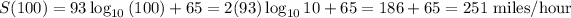
The average rate of change for the speed of the wind at the centre of a tornado will be

`S=251-158=93\text{ miles/hour}`

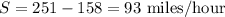
Hence, the average rate of change for the speed of the wind at the centre of a tornado from mile 10 to 100 is 93 miles/ hour

b) For the rate of change for the speed of the wind at the centre of a tornado from mile 100 to 1000,

Where, d = 100

`S(100)=93\log_(10)100+65=186+65=251\text{ miles/hour}_`

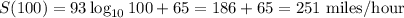
Where, d = 1000,

`S(1000)=93\log_(10)1000+65=3(93)\log_(10)10+65=279+65=344\text{ miles/hour}`

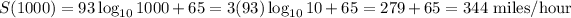
The average rate of change for the speed of the wind at the centre of a tornado will be

`S=344-351=93\text{ miles/hour}`

Hence, the average rate of change for the speed of the wind at the centre of a tornado from mile 100 to 1000 is 93 miles/ hour