Question

I need help finding out the missing side lengths for RQ and QP

Answer 1

The dimension of the triangle PQR given in the question is as shown below:

`\begin{gathered} RQ=\text{?},m\angle RQP=90^0 \\ QP=\text{?},m\angle QPR=60^0 \\ RP=4,m\angle PRQ=30^0 \end{gathered}`

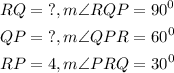
Using trigonometric ratio of sine of angle PRQ,

`\begin{gathered} \sin =\frac{opposite}{\text{hypothenuse}} \\ \sin 30^0=(QP)/(4) \\ QP=4*\sin 30^0 \\ QP=4*0.5000 \\ QP=2 \end{gathered}`

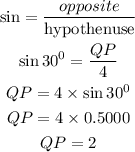
Since two sides are known, sides RP and QP, we can derive RQ using the Pythaogoras theorem as shown below:

`\begin{gathered} RP^2=QP^2+RQ^2 \\ 4^2=2^2+RQ^2 \\ 16=4+RQ^2 \\ 16-4=RQ^2 \\ 12=RQ^2 \\ RQ^2=12 \\ RQ=\sqrt[]{12} \\ RQ=3.464 \end{gathered}`

Hence,

RQ = 3.464 units

QP = 4 units