Hello!
We have the equation:
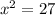
The first thing to solve it is to calculate the square root of each side, look:
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{27} \\ x=\sqrt[]{27} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/39v9tq046hcjeg5od0ph2k655iyof34ow4.png)
Let's calculate this square root by factorization:
![\sqrt[]{27}=+-3\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/xnu10dl25pt5iv2j425p27xb6q53ui3vdv.png)
Remember that when we talk about square roots, we must remember that we have two possible values: the positive and the negative. So, x will have two solutions, look:
![\begin{gathered} x_1=3\sqrt[]{3} \\ \\ x_2=-3\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/apa7svqt9t5lvgx0upk8ox5rxa5qm28y4m.png)
Answering your question, this equation has two solutions.