Question

Please help em find the missing angles for these triangles !

Answer 1

First of all, recall the trigonometric identities

`\sin (\theta)=(O)/(H)`
`\cos (\theta)=(A)/(H)`
`\tan (\theta)=(O)/(A)`

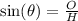
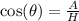
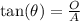
Where O = Opposite side, A = Adjecent side and H = Hypotenuse side

First Triangle:

As you can see, we know the angle and the adjacent side and the opposite side is unknown (x)

`\begin{gathered} \tan (32)=(x)/(13) \\ x=\tan (32)\cdot13 \\ x=0.62\cdot13 \\ x=8.1 \end{gathered}`

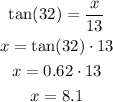
Therefore, the opposite side is 8.1

Second Triangle:

As you can see, we know the angle (37) and the adjacent side and the hypotenuse side is unknown (x)

`\begin{gathered} \cos (\theta)=(A)/(H) \\ \cos (37)=(11)/(x) \\ x=(11)/(\cos (37)) \\ x=(11)/(0.798) \\ x=13.9 \end{gathered}`

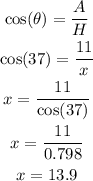
Therefore, the hypotenuse side is 13.9

Third Triangle:

As you can see, the angle is unknown but the adjacent and opposite sides are given so we can use the tan identity.

`\begin{gathered} \tan (\theta)=(O)/(A) \\ \tan (\theta)=(4)/(13) \\ \theta=\tan ^(-1)((4)/(13)) \\ \theta=17.1 \end{gathered}`

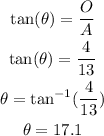
Therefore, the missing angle is 17.1