Question

You have 134,720 grams of a radioactive kind of actinium. How much will be left after 50 days if its half-life is 10 days?

Answer 1

Given:

The initial quantity of the actinium that will decay is 134720 grams.

Time, t=50 days

The half-life of the decaying quantity is 10 days.

To find the quantity that still remains after time t:

The half-life formula is given by,

`N(t)=N_0((1)/(2))^{\frac{t}{t_{(1)/(2)}}}`

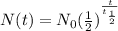
On substitution we get,

`\begin{gathered} N(50)=134720((1)/(2))^{(50)/(10)} \\ =134720*((1)/(2))^5 \\ =134720*0.03125 \\ =4210\text{ grams} \end{gathered}`

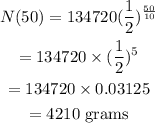
Hence, the quantity that still remains after time 50 days is 4210 grams.