Question

Suppose the Sunglasses Hut Company has a profit function given by P(q) = -0.03q^2 + 5q – 20, where ais the number of thousands of pairs of sunglasses sold and produced, and P(q) is the total profit, inthousands of dollars, from selling and producing a thousands of pairs of sunglasses.How many pairs of sunglasses should be sold to maximize profits?Round to the nearest whole pair of sunglasses.What is the maximum profit that can be expected?Round to the nearest cent.

Answer 1

STEP 1: Identify and Set Up

We are given a relation in form of a mathematical function and are asked to find the maximum value of the function.

This we will get by employing differential calculus to get the derivative of the function.

We know that at the maxima, the derivative equates to zero. This will aid finding the the no of units and employing back into the original function will give the maximum profit.

All these will be played out in step 2

Step 2: Execute

`\begin{gathered} p(q)=-0.03q^2+5q-20 \\ we\text{ then get the derivative p'(q)} \\ p^(\prime)(q)=-0.06q^{}+5 \end{gathered}`

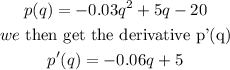
This p'(q) value is the function of the gradient at any point and at the maximum or minimum point, the gradient is zero (0). Therefore, we equate it to 0 and solve for q

`\begin{gathered} 0=-0.06q^{}+5 \\ \text{subtracting 5 from both sides} \\ -5=0.06q \\ \text{Dividing -0.06 from both sides gives:} \\ (-5)/(-0.06)=q=83.333 \end{gathered}`

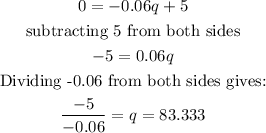
Therefore, the company will require roughly 83,333 pairs of sunglasses to make maximum profit.

To get the maximum profit, we now substitute this value of q into the function p(q) given thus:

`p(q)=-0.03(83)^2+5(83)-20=188.333`

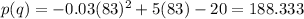
Therefore, the maximum profit, realized on the sale of 83,333 pairs of glasses is 188,330 dollars.