Question

Solve for x, y, and z. x =y =z =

Answer 1

We find z using Pythagorean's Theorem.

`\begin{gathered} z^2=10^(^2)+8^2 \\ z=\sqrt[]{100+64}=\sqrt[]{164} \\ z\approx12.8 \end{gathered}`

We find the acute angle between z and 10 using a sine function.

`\begin{gathered} \sin \theta=\frac{8}{\sqrt[]{164}} \\ \theta=\sin ^(-1)(0.62) \\ \theta\approx38.7 \end{gathered}`

Now, we find the angle between x and y using the interior angles theorem.

`\begin{gathered} 38.7+90+\beta=180 \\ \beta=180-90-38.7 \\ \beta=51.3 \end{gathered}`

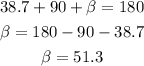
Then, we use the tangent function to find x.

`\begin{gathered} \tan \beta=(8)/(x) \\ x=(8)/(\tan 51.3) \\ x\approx6.4 \end{gathered}`

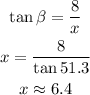
At last, we find y using Pythagorean's Theorem.

`\begin{gathered} y^2=x^2+8^2 \\ y=\sqrt[]{(6.4)^2+64}=\sqrt[]{104.96} \\ y\approx10.2 \end{gathered}`

Hence, z = 12.8, y = 10.2, and x = 6.4.