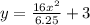SOLUTION
We are given the equations below:
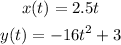
PART A
The marble will hit the ground when y(t)=0
![\begin{gathered} y(t)=-16t^2+3 \\ 0=-16t^2+3 \\ 16t^2=3 \\ t^2=(3)/(16) \\ t=\sqrt[]{(3)/(16)} \\ t=\frac{\sqrt[]{3}}{4} \\ t=0.4330\text{ seconds} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kqim8vvq4nsvd99ye95f8uc9iytzs00j89.png)
The marble will hit the ground after 0.4330 seconds
PART B
How far horizontally from the edge of the table will the marble first hit the ground can be gotten by substituting the value of t into x(t).
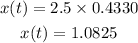
Therefore, the distance horizontally from the edge of the table the marble hits first is 1.0825feet
PART C
To express the parametric equations above the single rectangular equation, we eliminate t from both equations.
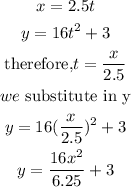
Therefore, the single rectangular equation is