Missing length of a triangle
We have the following triangle:
And we want to use the Sine Theorem in order to find the value of the side s.
We know, by this theorem, that if we divide one side with the sine of its opposite angle, we will obtain the same result:
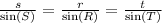
In this case we are going to select the sides s (because we want to find it) and r (because we already have its measure):
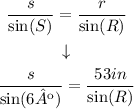
Finding R
In order to use the equation, we first have to find the value of the angle R.
Since the addition of all inner angles of a triangle is 180º, then
S + R + T = 180º
↓ replacing S and T
6º + R + 58º = 180º
↓ since 6º + 58º = 64º
R + 64º = 180º
↓ taking 64º to the right side
R = 180º - 64º
↓ since 180º - 64º = 116º
R = 116º
Then, we have
Finding s
Now, we can use the equation in order to find s:

Since
sin(6º) = 0.1045
sin(116º) = 0.8987
then

Then, we have that
s = 6.16 in
We want to round it to the nearest inch, which is 6.
Answer: s = 6