Question

Raj has a party length submarine sandwich of 48 inches. He wants to cut it into three piecesso that the large piece is 5 inches longer than the middle piece and the shortest piece is 8inches shorter than the middle piece. How long should each piece of the sandwich be?

Answer 1

Let 'x' represent the length of the middle piece

We were told that the large piece is 5inches longer than the middle piece,

Mathematically, it means

`x+5`

Also, we were told that the shortest piece is 8inches shorter than the middle piece.

Mathematically, it means

`x-8`

Therefore, the sum of all three lengths must be 48inches.

Hence,

`x+5+x+x-8=48`

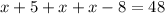
Solving for x

`\begin{gathered} x+x+x+5-8=48 \\ 3x-3=48 \\ 3x=48+3 \\ 3x=51 \end{gathered}`

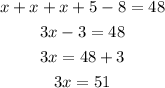
Divide both sides by 3

`\begin{gathered} (3x)/(3)=(51)/(3) \\ x=17 \\ \therefore The\text{ length of the middle piece=17inches.} \end{gathered}`

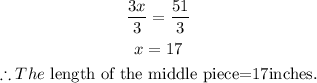
Therefore,

The length of the large piece is,

`\begin{gathered} x+5=17+5=22 \\ \therefore The\text{ length of the large piece is 22inches.} \end{gathered}`

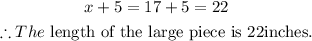
The length of the shortest piece is,

`\begin{gathered} x-8=17-8=9 \\ \therefore The\text{ length of the shortest piece is 9inches.} \end{gathered}`

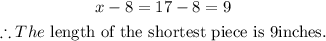
Hence, the lengths of the three-piece are 9inches, 17inches, and 22inches.