To graph using slope-intercept method, we have the line in the slope-intercept form:

m is the slope, this tell us how the function grows or decays from point to point. c is the intercept point. This is the point where the line crosses the y axis.
To graph it, we first locate the y-intercept: (0, -5) We mark that point, and then using the slope:
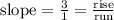
The function rises 3 units up and runs 1 unit right. Then:
Connecting the two points give us the graph of the function (note that the line should extend infinitely, but it's cutted in my draw)
Now to find if the point (3, -1) is a solution, we evaluate the value x = 3 and see if the output is y = -1:
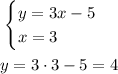
Thus, (3, -1) is not a solution