Find the equation of the line if inсlіnаtіоn 120°, у-intercept equal to - 6

Question

asked Oct 13, 2023 126k views

1 Answer

Leminhnguyen · Answer 1 · 2023-10-17T17:51:52+0000

The inclination is the angle of the line with respect to x-axis:

in our case, angle alpha is equal to 120 degrees:

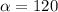
$\alpha=120$

The slope m in the line equation

is related to alpha by the tangent function, that is

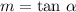
$m=\text{tan }\alpha$

In our case, we have

$\begin{gathered} m=\text{tan 120} \\ \sin ce\text{ tan120=-}\sqrt[]{3,}\text{ it yields} \\ m=-\sqrt[]{3} \end{gathered}$

So, our line equation has the form:

$y=-\sqrt[]{3}x+b$

where b is the y-intercept, which is equal to -6.

Finally, the line equation is

$y=-\sqrt[]{3}x-6$